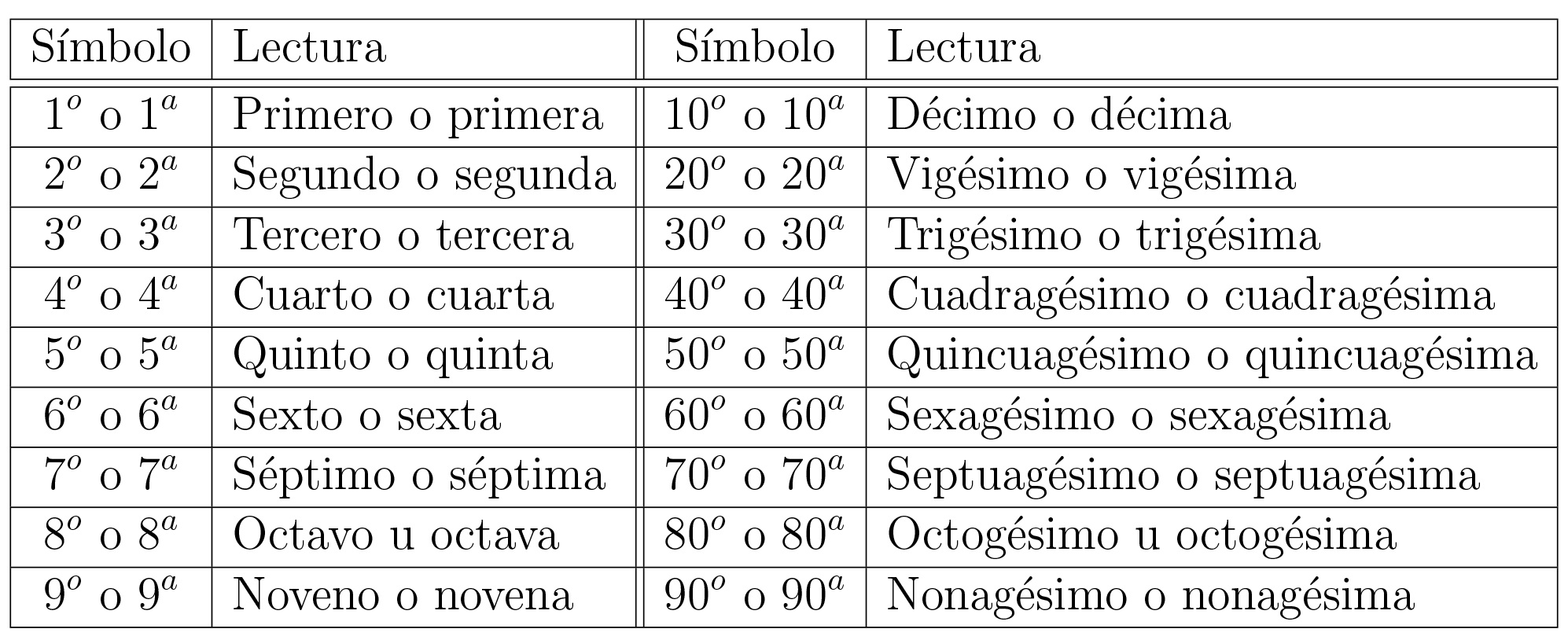
En matemáticas, un número ordinal es un número que denota la posición de un elemento perteneciente a una sucesión ordenada. Por ejemplo, en la sucesión a b c d, el elemento a es el primero, b el segundo, c el tercero, etc. Los números ordinales pueden generalizarse para las sucesiones infinitas, introducidas por Georg Cantor en 1897. El concepto de número ordinal, propio de las matemáticas, es también un concepto lingüístico (que es aquel que precisa la Real Academia Española). En este sentido, es aquel numeral que expresa la idea de orden o sucesión. Tiene género ("primero" / "primera") y puede aparecer apocopado ("primer"). En el lenguaje corriente no se utilizan habitualmente sino hasta el 10 o 12, y para los superiores se usa el cardinal correspondiente: siglo diecinueve, Juan XXIII (veintitrés).1 Más adelante se detallan en su denominación más propia.
Los números cardinales se pueden emplear para cuantificar el tamaño de un conjunto (finito o infinito), mientras que los números ordinales pueden emplearse para describir la posición de un elemento en una sucesión (finita o infinita). Cuando se trata de conjuntos finitos, los números naturales, los ordinales y los cardinales coinciden, es decir, son básicamente identificables. En el caso de conjuntos infinitos la situación es más complicada y hay que distinguir entre ordinales y cardinales (además, para conjuntos infinitos los números naturales no son de utilidad). El aspecto del tamaño de un conjunto se describe mediante números cardinales, que también fueron descubiertos por Cantor, mientras que el aspecto de la posición se generaliza mediante los números ordinales, los cuales analizaremos aquí.
En la teoría de conjuntos, los números naturales se suelen construir como conjuntos tales que cada número natural es el conjunto de todos los números naturales más pequeños:
Visto así, cada número natural es un conjunto bien ordenado: por ejemplo, el conjunto del 4 tiene los elementos 0, 1, 2 y 3, que por supuesto se ordenan 0 < 1 < 2 < 3, y éste es un buen orden. Un número natural es menor que otro si y solo si es un elemento del otro.
Bajo esta convención, se puede demostrar que todo conjunto finito bien ordenado es ordenadamente isomorfo a exactamente un número natural. Este isomorfismo motiva a generalizar esta construcción hacia los conjuntos no finitos y sus correspondientes números que serían más grandes que cualquier número natural.